Some years ago I became aware that the so-called “Fig.9”
knot has an alternative form that provides some useful
and interesting knots --i.p., a non-jamming stopper knot
(which might serve mid-line uses in by-hand climbing
ropes or in dockline markers), and a TIB eye knot. The
end-2-end corresponding knot can be seen as shortened
(and thus to mere overhands in this brevity) to ABOK #1425
–which I feel is a knot deserving fuller appreciation/usage.
At some point, I fiddled another symmetric form of the Fig.9
and found --to my surprise-- that it, too, provided a potentially
useful mid-line stopper knot (not sure about anything further)!
So, eventually I made some sketches to illustrate the lower
members of what can be seen as a series beginning with a
degenerate form in the overhand (it doesn’t provide so many
distinct orientations). I’ve not looked for useful knots beyond
the fig.9 (but for the fig.10’s asymmetric form’s use qua
end-line stopper (viz., the stevedore knot) and also an eyeknot
& directional eyeknot. My feeling is that the further entanglements
of the series members beyond fig.10, surely, just get in the way
of realizing practical structures.
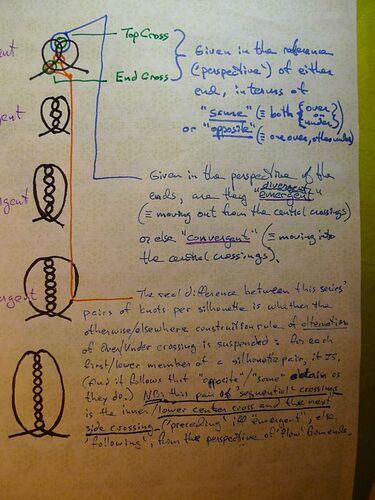
Attached are four photos of my knot-notes pages with some of
these knots illustrated. The first two photos combine to present
a single page in which I attempt --with some clumsiness, left in–
to set out the series perspicuously. This page attempts some
economy of illustration by using silhouettes to represent pairs
of tangles. I’m afraid that my initial labeling of respective members
of each pair by “opposite” and “same” is reversed from what it
should be, given the better scheme, indicated by my text pointed
to by the orange line --which labels work for either of the two
symmetric forms shown (side-twists or center-twist, resp.).
(Note that the leftmost lowermost two silhouettes are in the
wrong order --as indicated there, by arrows–, but correctly
identified as “15 & 16”, “13 & 14”.)
Also, my labels “emergent” / “convergent” refer to whether
the flow into the tangle from the ends emerges upwards
to the sides, or rather comes from the sides to converge
in that pair of center crossings.
However, this all might benefit from further & saner thinking.
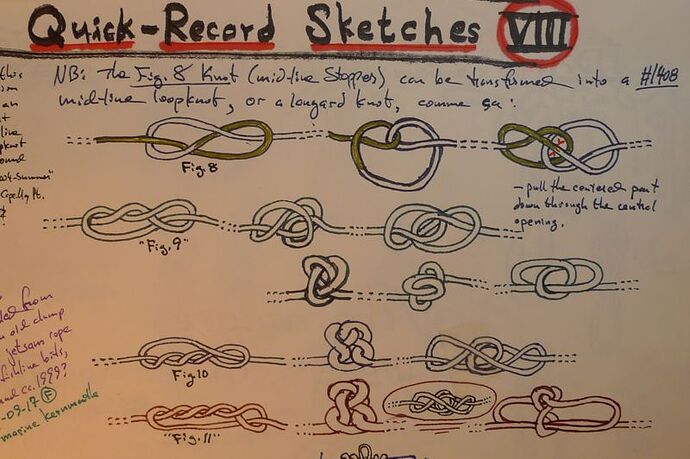
The 3rd image is of earlier fiddlings in which I found that the
knots could lead to min-line eye knots (though not TIB), and
these have been shown from fig.8 .. 11 (the overhand
tangle provides for what might be called a grass-bend/whatknot
mid-line eyeknot --potentially collapsable into a buntline hitch).
And in the case of the fig.9, I show an effective transformation
from the asymmetric (and well-known, stevedore-like) form
to the side-twists form --a transition that I long knew was
possible, but which often eluded my best efforts, driving me mad!
Finally, the fourth image shows the conversion from the center-twist
tangle into a usable stopper-knot form, which is easily loosened!
(I think that my remark about “stubbornly refusing to go …”
refers to trying to reach the other form, of #523, side-twists.)
It’s not clear to me that this knot can well endure one-sided
loading (the canonical end-stopper loading)