The relationship between 'bends' and eye knots

Knotting Concepts & Explorations
61

Quote from: agent_smith on November 01, 2024, 12:10:24 AM
EDIT NOTE:

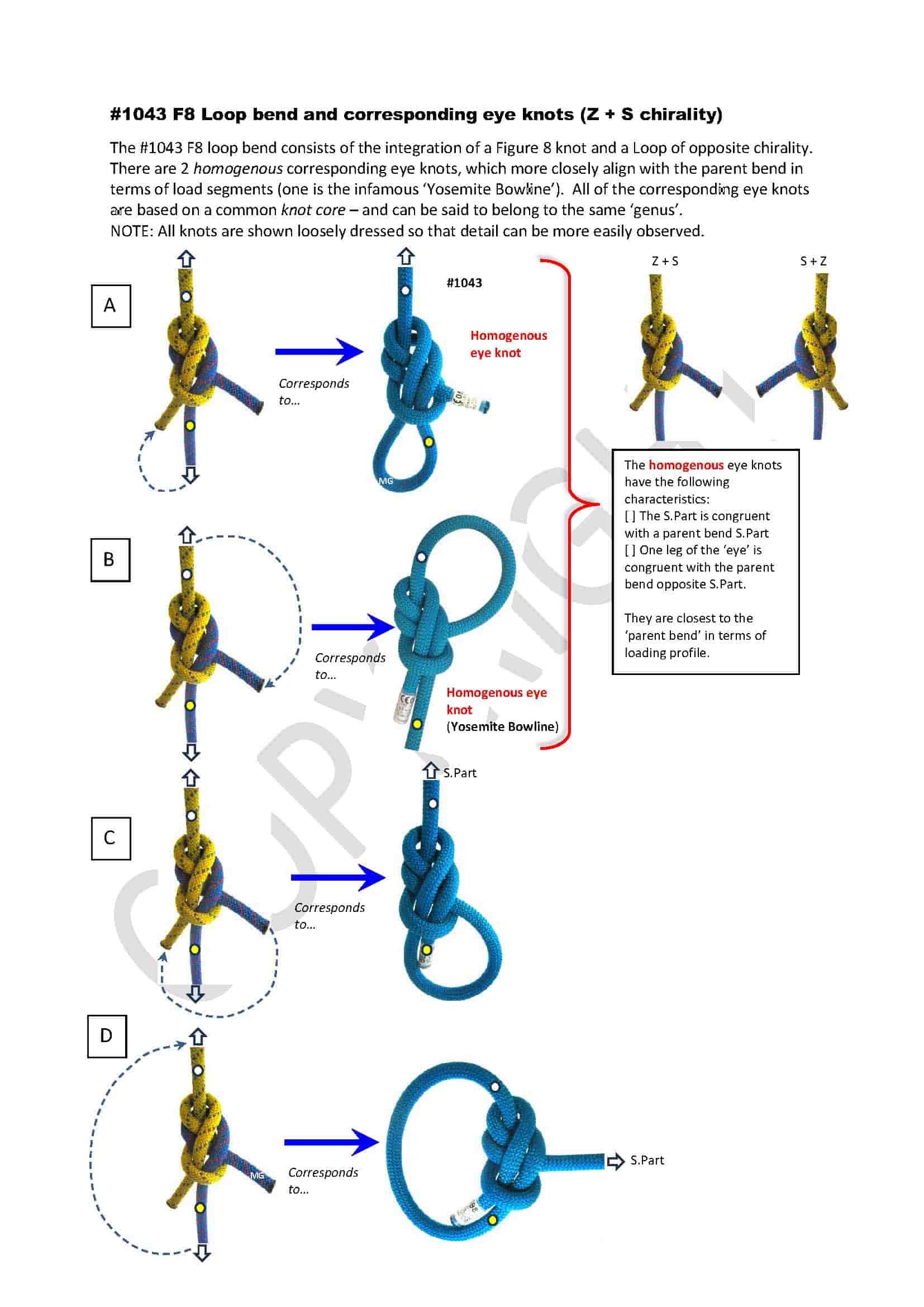
I've added an image showing #1043 and the other corresponding eye knots that have been derived from the 'parent bend'. One of the corresponding eye knots is in fact the infamous 'Yosemite Bowline'.
You break a rule of correspondence in this set with the 4th one as it alone has a parent Tail qua S.Part. In Tangle designations, with your yellow rope = "1-2" and the blue rope = "A-B",

You appear to be quoting from your personal correspondence ‘rule’ book?
I didn’t know that any such ‘rules’ existed?
In any case, you are not making any sense.
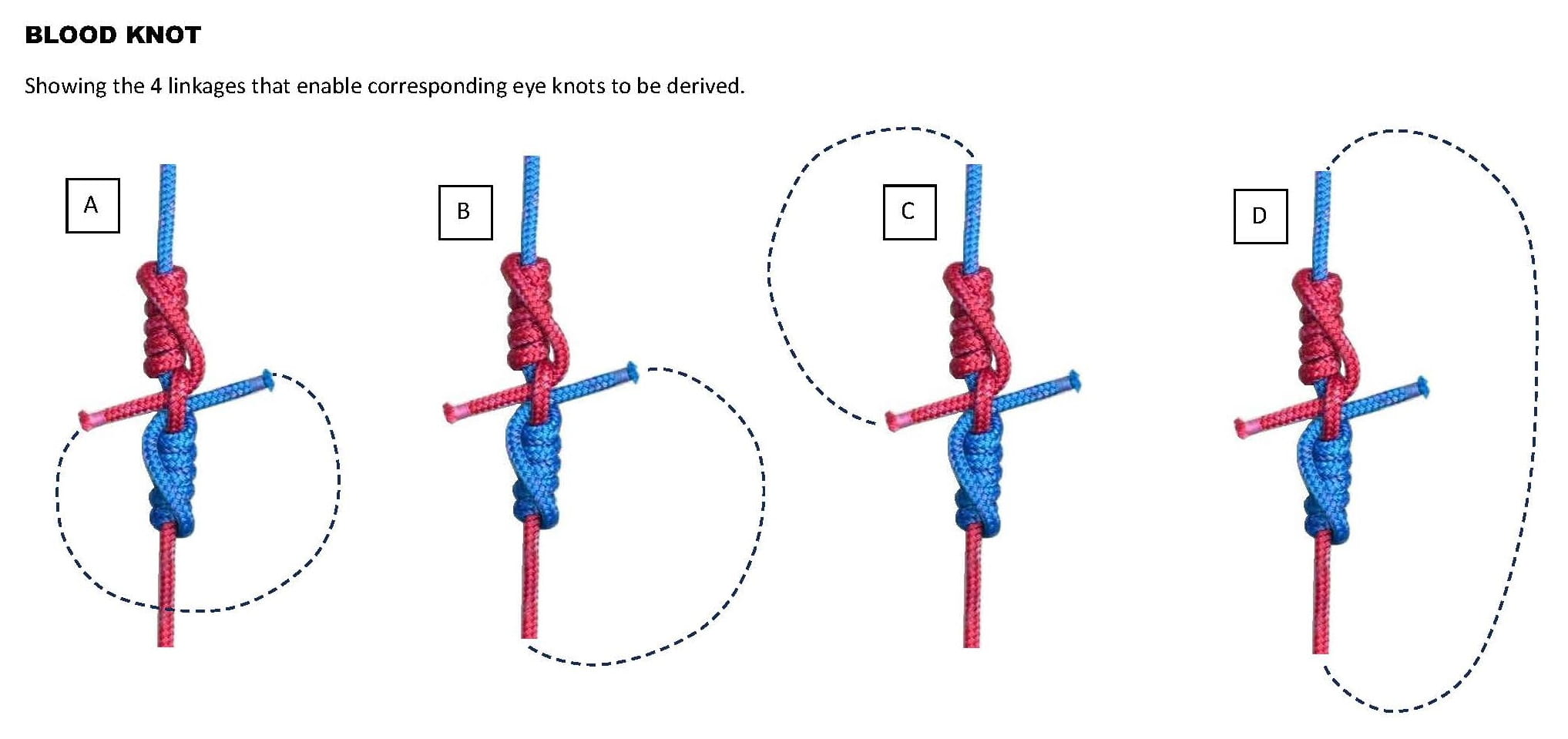
I am simply showing the 4 corresponding ‘eye knots’ which are derived
from the linkages that can be made from the source ‘parent bend’.
Image ‘D’ is simply one of the linkages that can be made.
There is also a transposition that can be made of image ‘D’,
by changing the identities of the S.Part and tail end.
I am only showing 4 ‘eye knots’, I am not also showing a further
4 transpositions.

(Btw, "C" looks dubious of blue-rope/REL->Tail security; I'd put in another tuck of some kind if trying this!)
? Deriving and showing the corresponding 'eye knots' has nothing to do with knot stability or viability. You seem to be focussing on something different to me. I am [u]preserving the geometric relationship[/u] between 'parent bend' and its corresponding 'eye knot'. The viability/stability of the derived 'eye knots' is irrelevant for this theoretical exercise.

I had stated previously in other posts that not all of the derived corresponding ‘eye knots’
will be stable/viable.
I would point out that the process of deriving, tying, and then showing the corresponding
‘eye knots’ is interesting because it reveals some emergent properties.
New discoveries can be made.

62

From Dan Lehman:

"a good example":: well, in fact what brought this idea to mind, for me, reading of the "2-by1 knot"[?! --name not sure] in Stanley BARNES's 1951 ed. Angler's Knots :: ... reply from agent smith:
This makes it difficult for readers to follow your ideas.

But readers should know the Blood Knot of anglers,
and otherwise can find it.
from agent smith:

Well yes, now that you mention 'blood knot', readers can begin to make sense of this.

To that, one need only
follow the words and form the joint 1 line-vs-2.
The version of the Blood knot that works simplest
would take the two ends’ Tails and fuse them;
then you cut off one S.Part to amount of material
for fold back to form the eye,
and run it back twin to its extant course.
(In practice, one will I think want fewer of the
binding wraps from EACH eye leg, summing to
about the number in the S.Part’s wrapping.

Following your words can be complicated.
But now that you’ve identified ‘Blood knot’ - it makes it somewhat
easier to illustrate what you suggest.
And so I have attached an image of a ‘parent Blood knot bend’ and
its corresponding eye knots.

Image ‘A’ is what you were attempting to explain (I think).
And yes, fewer wraps/turns would make sense.

BLOOD KNOT_corresponding eye knots_WEB.jpg

63

  1. You don’t have a proper Blood knot, but only the
    corruption wrought by those who cannot attend to
    getting things right. You depict what Barnes calls
    the “out-coil” tying method prior to its being set
    hard and converting all of those out-coiling wraps
    into overwraps with the culmination of the Tail
    betting tucked out of the center.

  2. My words were clear :: tie a Blood knot of one
    line (S.Part’s) to a U-FOLD’s >>> TWO <<< ends
    –the “2-to-1” aspect-- ;
    THEN fuse one of these twin eye bight (U-fold) ends
    into the S.Part’s tail,
    converting the two distinct lines into a single line
    with Blood-Knot loading geometry, albeit with the
    eye-legs in tandem being the one half opposite the
    S.Part’s single strand’s wraps.

And this knot is roughly what you show as “B”,
but, again, you need to fuse the tails :: the eye’s
leg exit the eye-side of the knot twinned as they
are in their binding wraps (and thus which wraps
per strand should be fewer than the S.Part’s).

–dl*

64

per Dan Lehman in relation to the image of a ‘Blood knot’

1) You don't have a proper Blood knot, but only the corruption wrought by those who cannot attend to getting things right.
Wow - the image is from Grog's website (animated knots). Link: https://www.animatedknots.com/blood-knot Have you contacted Grog to advise him of his error?

and this:

You depict what Barnes calls the "out-coil" tying method prior to its being set hard and converting all of those out-coiling wraps into overwraps with the culmination of the Tail betting tucked out of the center.
Netknots have this link: https://www.netknots.com/fishing_knots/blood-knot

per Dan Lehman knot tying explanation:

2) My words were clear :: tie a Blood knot of one line (S.Part's) to a U-FOLD's >>> TWO <<< ends --the "2-to-1" aspect-- ; THEN fuse one of these twin eye bight (U-fold) ends into the S.Part's tail, converting the two distinct lines into a single line with Blood-Knot loading geometry, albeit with the eye-legs in tandem being the one half opposite the S.Part's single strand's wraps.

And this knot is roughly what you show as “B”,
but, again, you need to fuse the tails :: the eye’s
leg exit the eye-side of the knot twinned as they
are in their binding wraps (and thus which wraps
per strand should be fewer than the S.Part’s).

As others have commented in other posts elsewhere, it might be
helpful to your cause if you took a photo and posted it.
It will also reduce the back n forth posts with you admonishing
and/or correcting tying mistakes made by people who are acting
in good faith to try to assemble your geometric word puzzle!

EDIT
I’m away for the next 5 days and wont have much spare time to
decipher and tie your knot from your description. So a
photo will significantly aid in understanding.
Is requesting a photo an insurmountable task?

65

[you omitted the full text]
…

you show
[A] 1-vs-2+A (most commonly seen correspondence),
[C] … +B (your 3rd , RELeg being former Tail)

[B.] A-vs-B+1 (your 2nd)
[na] … +2 (4th case missed of this logical sequence.
with you showing
[D] B-vs-A+1 (A-B’s Tail vs. two parent S.Parts)

I thought YOUR rule was that “principal” EKs would
have one parent joint S.Part loaded? Your set of four
lacks this quality in the 4th case.
You give the two parent S.Part cases for the yellow rope
but only ONE for the blue rope --as I note above,
you do not have the EK with the blue rope S.Part.

–dl*

66

OK, I think I’m getting an even/clear picture of our
problems. You’ve used special meanings for “primary”
& “principal”, of which I’m a bit unsure, except that
the latest for “primary” is that one e2e/“parent” S.Part
must be the EK’s S.Part, and the other must be an eye leg.
So, for my e2e of 1-v- A (your S-1 v S-2),
there will be in the EK ::
1 -v- 2+A
(S-1 v T-1 + S-2)
&
A -v- B+1
(S-2 -v- T-2 + S-1).

When you set out linkages, yes, there are 4 ; but they
alone do NOT show an EK --for a EK S.Part remains to
be chosen of the 2 unlinked ends. In your seeking
“primary”, you have chosen the unlinked S.Part and
not the unlinked Tail for this, which of course makes sense.

But when you have the linkage of the 2 Tails (T-1 + T-2,
my “2 + B”), there is no clear rule/guide --other than
what I take is you just making some assessment that
one loading is better than the other (is this always
the case, and does the quality of the loading come
into the assessment?), and ignore the other
–you have S.1 making an EK with the linked Tails,
but not S.2.
If S.2 is ALSO presented as one of the corresponding
EKs, then you have in your 1st 3 linkages all of the cases
where one or other Joint S.Part is an EK S.Part
(S+T twice, involving each parent S.Part;
and now T+T twice, w/each parent S.Part involved).

And so the 4th linkage (S + S) is non-primary … .
Consider if you put the #1043 e2e Joint upside-down,
and then follow the linkages as shown above :: the first
two EKs are there but come in reverse order,
and the 3rd one --case “C”-- gives a different knot
than is got from the first orientation of #1043 Joint.

.:. IMO, this breaks your model.

As for “a further 4 transpositions”, there is simply
a choice of other unlinked ends as S.Parts. I.e.,
I see no reason to invoke a concept of transposition
for these, but that they just follow from the logic
of the linkages & available unlinked ends to take
the S.Part/Tail roles; and maybe we can call these
“secondary” or something.

–dl*

67

To my audience of one (Dan Lehman):

OK, I think I'm getting an even/clear picture of our problems.

As far as I know, I am the first to tackle this subject matter head-on
in fine detail - to evolve a theoretical model.
I acknowledge Harry Asher’s beginnings in his book (The Alternative Knot Book),
but he only briefly touched on the subject.

You've used special meanings for "primary" & "principal", of which I'm a bit unsure, except that the latest for "primary" is that one e2e/"parent" S.Part must be the EK's S.Part, and the other must be an eye leg
Yes - I have tried to use specific words to describe specific things. Its complicated.

Its sort of like the issue with ‘Bowlines’ - where I have tried to
develop a theoretical model of what [a] ‘Bowline’ is. I have tried to
establish tighter rules for defining which knots can be classified as ‘Bowlines’.
You seem to be more liberal in allowing the flood-gates to be
opened to a w-i-d-e-r definition.
Whereas I prefer a more narrow definition.
I have settled on the term “Quasi Bowline” to describe those eye knots
who resemble a ‘Bowline’ but do not have all the geometric elements
necessary to qualify as a ‘Bowline’.

Okay - to the issue at hand:

You seem to be in agreement that with an end-to-end join (‘bend’)
involving the unification of 2 separate ropes/cords:
Four linkages can be made between the S.Parts and Tail ends.
These linkages allow the creation of ‘eye knots’.
These ‘eye knots’ are derived from, and related to the parent bend.
At this point, it can be pointed out that not all of the derived eye knots will be viable/stable.
I am confining myself to a geometric relationship with the parent bend.

Some of these derived ‘eye knots’ will have a closer relationship to the parent bend in terms
of loading profile.

is that one e2e/"parent" S.Part must be the EK's S.Part, and the other must be an eye leg
Yes. [u]Formulation:[/u] 1. The S.Part of the derived 'eye knot' is congruent to an S.Part of parent bend. 2. One leg of the derived 'eye knot' is congruent with the opposite S.Part of the parent bend.

I think the best way to describe these particular derived ‘eye knots’ is to use the term; Homogenous.
For now, I’ll refer to these ‘eye knots’ as being homogenous to the parent bend.

With regard to the 4 corresponding eye knots derived from the 4 linkages:
Each can undergo a transposition - where the S.Part and Tail end change identities.
We can also think of this as a reversal of polarity.
Again, not all of these transposed ‘eye knots’ will be viable/stable.

And this is where the number 8 originated (4 + 4).

IMO, this breaks your model.
Not sure where you got your inspiration for making this claim?

I never specified how many derived ‘eye knots’ would be homogenous to the parent bend.
I expect that some derived ‘eye knots’ would be homogenous, and some not.
I have yet to crack the code for determining how to figure this out.

I will also state that some derived ‘eye knots’ may be identical twins.
I have no formulation to predict this.
Its a work in progress.

Perhaps you could advance a theory for predicting if a given parent bend will produce
a set of identical twin ‘eye knots’?

68

Why do you miss the explicit reason given???
You don’t have a good model if you get different
results depending upon which S.Part of the Joint
you put top/bottom --the “corresponding” EKs should be
the same, either way. I clearly pointed out how
you get different results in your 4.

–dl*

69

To Dan Lehman:

Why do you miss the explicit reason given??? You don't have a good model if you get different results depending upon which S.Part of the Joint you put top/bottom --the "corresponding" EKs should be the same, either way. I clearly pointed out how you get different results in your 4.
I didn't "miss" anything.

There’s lots of “you” and “your” in your narrative.

It appears that you might be referring to my presented #1043 Loop bend?
Refer image below as a reference to this post.
As with all ‘bends’ formed from the unification of 2 ropes, there are 4 available linkages.
I had presented the 4 corresponding ‘eye knots’ derived from the parent bend.

You appear to be making a lot of noise about the 4th (last) derived eye knot?
It is labelled “D” (ie image D).

And you are making claims of ‘rule breaking’ or ‘model breaking’ - resulting in the
end of the known knotting universe.

My current best formulation for ‘homogeneity’ is as follows:

  1. The S.Part of the derived ‘eye knot’ is congruent to an S.Part of parent bend.
  2. One leg of the derived ‘eye knot’ is congruent with the opposite S.Part of the parent bend.

My presented image “D” is therefore not homogenous to the parent bend.
And the presented image “C” is also not homogenous to the parent bend.

No universe ending paradox’s here…

NOTE:
All images can both undergo a reversal of polarity to transpose
the S.Parts and Tail ends.
In any transposition, there is no guarantee that the resulting eye knot will be viable/stable.
And so obviously image “D” can undergo a transposition.

You don't have a good model if you get different results depending upon which S.Part of the Joint you put top/bottom --the "corresponding" EKs should be the same, either way. I clearly pointed out how you get different results in your 4.
Your claims here don't disturb the fact that there are 4 possible linkages. With specific regard to the 4th image "D": There's no up/down or top/bottom per se. There's simply a linkage that can be made. In image "D" the linkage occurs between the S.Parts of the original parent bend. I chose to make the [b]blue [/b]exiting tail of the original parent bend an S.Part of the derived 'eye knot'. Remember that a [i]transposition [/i]can be made to reverse the polarity. The reversal of polarity does not alter the [i]linkage [/i]made between the original S.Parts.

F8-Loop-bend_1043_corresponding eye knots_WEB.jpg

70

As I clearly previously stated --which you keep ignoring–
the issue is with your THIRD image “C” :: there are TWO
possible EKS and you show/count just one (with the yellow
S.Part) ignoring that other (blue S.Part). This is a linkage
that retains one e2e Joint S.Part qua S.Part, important
to the model.

Had you turned each given #1043 image upside-down,
Blue S.Part upper, Yellow lower,
you’d get the 1st two --Primary-- cases but in reverse
order, then you’d get the missed case for “C” and miss
the one got above. That breaks your model.

–dl*

71
As I clearly previously stated --which you keep ignoring-- the issue is with your THIRD image "C" :: there are TWO possible EKS and you show/count just one (with the yellow S.Part) ignoring that other (blue S.Part).
[b]With specific regard to image "C" (3rd image):[/b] There are a total of 4 possible linkages. The linkage shown for image "C" is correct. A transposition can be made which reverses the polarity (ie tail and S.Part change identity). If the 'tail end' now becomes the new S.Part, it wont be homogenous to the parent bend. The 'eye' of the 'eye knot' doesn't have homogeneity relative to the parent bend.

Your assertions about ‘model breaking’ doesn’t make sense to me.
The ‘model’ for homogeneity goes like this:

  1. The S.Part of the derived ‘eye knot’ is congruent to an S.Part of the parent bend.
  2. One leg of the derived ‘eye knot’ is congruent with the opposite S.Part of the parent bend.

And so condition 2 above wont be fulfilled.
The legs of the ‘eye’ are not congruent with any S.Part from the parent bend.
Therefore, for image “C”, the derived ‘eye knot’ (including its transposed form)
wont be homogenous to the parent bend.

Same goes for image “D”.
The derived ‘eye knot’ is not homogenous to the parent bend.
And neither is its transposed form.

With regard to images “A” and “B”:
They are homogenous to the parent bend.
However, their transposed forms are not.

…

There might be some difference in how we interpret transposition.
For each of the ‘eye knots’ derived from the 4 linkages, there will also be a
transposed form where the ‘polarity’ has been reversed.
This is where an S.Part and tail change identity.
What was previously an S.Part, now becomes a tail end (and vice versa).
However, the core geometry of the knot does not change - it remains the same.

…

EDIT NOTE:

Had you turned each given #1043 image upside-down, Blue S.Part upper, Yellow lower, you'd get the 1st two --Primary-- cases but in reverse order, then you'd get the missed case for "C" and miss the one got above. That breaks your model.

I chose to illustrate the parent bend in the particular orientation depicted.
That is, yellow S.Part is ‘up’ and blue S.Part is ‘down’.
In principal, I dont agree with the concept of ‘up’, ‘down’, ‘left’, and ‘right’.
I always imagine I am tying knots inside the international space station, where there is no ‘up’ or ‘down’.

However, there is usually a logical way of orienting a knot to show its geometry.
I chose to orient the parent bend in the way I did to align with Ashley’s #1043.
It was logical to do so.
The core geometry of the ‘bend’ is undisturbed by orientation.
It doesn’t matter which way the knot is tilted or oriented, the core remains unchanged.

I might also comment that there is a practical reality of the effects of load.
When load is applied, we can see how the knot responds (eg is it stable?).

In the derived ‘eye knot’ in image “C”, if we transpose and reverse the polarity,
the knot becomes unstable.
I had mentioned several times previously that there is no guarantee that a transposed
‘eye knot’ will be stable. In fact, in many instances, a transposition results in instability.

72

Yes, but the “corresponding KNOTS” count is 1 short of correct => 2,
one w/S.Part Yellow, other with S.Part Blue.

A [i][b]transposition [/b][/i]can be made which reverses the polarity (ie tail and S.Part change identity). If the 'tail end' now becomes the new S.Part, it wont be homogenous to the parent bend. The 'eye' of the 'eye knot' doesn't have homogeneity relative to the parent bend.
Prior to any thoughts of transposition comes getting the thing to be transposed :: in the Case of LINKAGE "C" there are TWO ***KNOTS*** to be had, one for each of the e2e S.Parts. And each is as or as-not "homogenous" to the joint as the other --they have "congruent" S.Parts (one for Yellow, one for Blue), and e2e Tails for the linkage'd eye legs.
Your assertions about 'model breaking' doesn't make sense to me. [u]The 'model' for homogeneity goes like this:[/u] 1. The S.Part of the derived 'eye knot' is congruent to an S.Part of the parent bend. 2. One leg of the derived 'eye knot' is congruent with the opposite S.Part of the parent bend.
Applying your case of the 4 linkages in #1043-Joint with EACH image turned upside-down (so, Blue S.Part up), you would have a blue-S.Part'd case C and miss what you have above :: THAT shows that applying whatever it was you thought you were doing doesn't get the proper same-knots output (since orientation of e2e parent shouldn't matter).

–dl*

73

To Dan Lehman:

I’m struggling to understand your position - and find myself in disagreement with you.

I think we need to go back to the foundations of the theory - and work from there.

In relation to end-to-end joins (‘bends’):

  1. There can only be four (4) linkages produced between the S.Parts and Tail ends.
  2. Eye knots can be derived from these four linkages.
  3. The choice of S.Part and Tail end, and spatial orientation for each of the 4 derived eye knots is based on a geometric relationship with the parent bend.
  4. Each of these derived eye knots can undergo a transposition to reverse the polarity, where the S.Part and Tail end change identity.
  5. There is no ‘up’ or ‘down’ in examining the relationship between bends and eye knots (imagining the knot tyer is located in the international space station).
  6. Some of the derived eye knots will be homogenous relative to the parent bend (ie their loading profile will be closer in alignment relative to the parent bend).

Rules for homogeneity:

  1. The S.Part of the derived ‘eye knot’ is congruent to an S.Part of the parent bend.
  2. One leg of the ‘eye’ of the derived ‘eye knot’ is congruent with the opposite S.Part of the parent bend.
    (NOTE: It is possible that you misunderstood rule #2 above. An ‘eye’ has 2 legs. One leg of the ‘eye’ is congruent with an S.Part).
    …

I’ll stop here.

What I request that you do is to examine what I have written, and determine if you agree (or not).
Forget about any presented images for this exercise… just look at the definitions I have written.

74

… and you keep ignoring what I write.

1. There can only be four (4) linkages produced between the S.Parts and Tail ends.
  1. Eye knots can be derived from these four linkages.
  2. The choice of S.Part and Tail end, and spatial orientation
    for each of the 4 derived eye knots is based on a geometric relationship with the parent bend.

HERE is your problem, going from 4 linkages to
“each of the 4 derived EKs” !!
How does one derive an EK from a Linkage
–you don’t say, and you keep missing the point
that THIS aspect isn’t well formulated,
that TWO EKS are derivable from each of the
four LINKages (possibly via knot symmetry
there will be duplicates).
4. Each of these derived eye knots can undergo a transposition to reverse the polarity, where the S.Part and Tail end change identity.
But, rather & prior any derived EK undergoing a "transposition", it ... has to be DERIVED :: and you have no fixed way that the derivation is made --AS I KEEP POINTING OUT TO YOU OVER & OVER, in e.g. Linkage Case C there are TWO EKs that can be derived --with either the Yellow (shown) or Blue (missed) rope qua S.Part--, you choose the Yellow S.Part, and ignore the Blue.

–dl*

75

Dan, take a stress pill :slight_smile:

HERE is your problem, going from 4 linkages to "each of the 4 derived EKs" !! How does one derive an EK from a Linkage --you don't say, and you keep missing the point that THIS aspect isn't well formulated, that TWO EKS are derivable from each of the four LINKages (possibly via knot symmetry there will be duplicates).
I see your problem. You are confused.

There are only 4 possible linkages.
Eye knots are derived from these 4 linkages.
Where you spiral into the abyss is choosing how to
orient the ‘eye knots’.

You seem to miss the key point that all ‘eye knots’
are derived from the 4 linkages.

How does one derive an EK from a Linkage
Your fixation is how the initial 4 'eye knots' are derived/chosen. And you think the choice of the initial 4 'eye knots' is a model breaking paradox?

The obvious answer to your paradox is that it actually doesn’t matter!
You can think of this as quantum entanglement.
Imagine 2 entangled photons in a state of superposition.
One photon has ‘up’ polarisation and the other has ‘down’ polarisation.
If we measure one photons polarisation, we immediately know what the other
photon will be.

And so the choice of 4 initial ‘eye knots’ will have a certain polarisation (polarity).
Each of these initial ‘eye knots’ will have an opposite polarisation, where the
S.Parts and Tail ends undergo a transposition and change identity.

An alternative way to look at this paradox is that the initial choice of the 4 ‘eye knots’
polarity is based on logic. That is, the particular choices of orientation will naturally
align with the parent bend. And so the loading profile will be closely aligned with and
‘homogenous’ to the parent bend.

Some of the derived ‘eye knots’ will be homogenous to the parent bend.
Some wont.
Selecting on the basis of achieving homogeneity is logical.

But, rather & prior any derived EK undergoing a "transposition", it ... has to be DERIVED :: and you have no fixed way that the derivation is made --AS I KEEP POINTING OUT TO YOU OVER & OVER...
Yes - I feel your pain. You need to overcome your irritation by realising that it actually doesn't matter what choice of orientation/polarisation is initially made with each of the 4 'eye knots'. Because - for each choice that is made, there will also be an opposite polarity. You still end up with the same total head count - eight (8) 'eye knots'.

There is no model breaking paradox.

How does one derive an EK from a Linkage?
[u]Again - in as few words as I can muster:[/u] There are 4 possible linkages that can be made from any given 'parent bend'. We can immediately create 4 corresponding 'eye knots' from these linkages. Each derived 'eye knot' will have a certain polarisation/polarity. The choice of polarity will be based on achieving [i]homogeneity [/i]relative to the parent bend. And if homogeneity can't be achieved, then a geometric approximation can be made. And so the initial 4 derived 'eye knots' are the most logical choices.

Hopefully you can see that regardless of initial choice of orientation/polarisation,
the total head count will still be eight (8) ‘eye knots’.

Amen.

76

Stop being a pill.

HERE is your problem, going from 4 linkages to "each of the 4 derived EKs" !! How does one derive an EK from a Linkage --you don't say, and you keep missing the point that THIS aspect isn't well formulated, that TWO EKS are derivable from each of the four LINKages (possibly via knot symmetry there will be duplicates).
I see your problem. You are confused.
No, you confuse my points in steadfastly refusing to see YOUR system's problem.
There are only 4 possible linkages.
Yes, I've not said otherwise; 4 linkages.
Eye knots are derived from these 4 linkages. Where you spiral into the abyss is choosing how to orient the 'eye knots'.
No, I argue that there's no stated rule/method on how to DERIVE the supposed "4" --only-- "principle"? EKs.
You seem to miss the key point that all 'eye knots' are derived from the 4 linkages.
Of course I doN'T say otherwise; but I DO say that their is no method for choosing 4 and just 4, and which are the 4.
How does one derive an EK from a Linkage
Your fixation is how the initial 4 'eye knots' are derived/chosen. And you think the choice of the initial 4 'eye knots' is a model breaking paradox?
Well, if you have a different foursome than another e2e-TO-EKs evaluator, yes, that IMO breaks your model with its failure to guide both evaluators to the same Four.
The obvious answer to your paradox is that it actually doesn't matter!
Really? So we'll have different "4 primary/principle/ EKs"?
And so the choice of 4 initial 'eye knots' will have a certain polarisation (polarity). Each of these initial 'eye knots' will have an opposite polarisation, where the S.Parts and Tail ends undergo a transposition and change identity.
Distinct loadings give distinct knots. You don't care about deriving some "principle" Four, just take one EK from each Linkage? Yes, there are 8 EKs to be had from all possible loadings; but you seem to have some idea of discriminating a (Fab) Four.

To this you say ::

... the initial choice of the 4 'eye knots' polarity is [u]based on logic[/u]. That is, the particular choices of orientation will naturally align with the parent bend. And so the loading profile will be closely aligned with and 'homogenous' to the parent bend. // Some of the derived 'eye knots' will be homogenous to the parent bend. Some won't. Selecting on the basis of achieving [i]homogeneity [/i]is logical. [[def. Rules for [i]homogeneity[/i]: | 1. The S.Part of the derived 'eye knot' is [u][i]congruent [/i][/u]to an S.Part of the parent bend. | 2. One leg of the 'eye' of the derived 'eye knot' is congruent with the opposite S.Part of the parent bend. ]]
If I understand your idea of [i]"homogeneity"[/i], that covers just TWO EKs --i.p., those with matching S.Parts AND the Returning Eye Leg.
( "(NOTE: It is possible that you misunderstood rule #2 above. An 'eye' has 2 legs. [u]One leg of the 'eye' is congruent with an S.Part[/u]).
And you should understand that only the Returning Eye Leg can be this!

Now, about the other Two of
the Fab Four.

But, rather & prior any derived EK undergoing a "transposition", it ... has to be DERIVED :: and you have no fixed way that the derivation is made --AS I KEEP POINTING OUT TO YOU OVER & OVER...

And if homogeneity can’t be achieved, then a geometric approximation can be made.
And so the initial 4 derived ‘eye knots’ are the most logical choices.


Which is more “logical” : an EK with
its S.Part one of the Joint’s,
and eye legs the Joint’s Tails;
or an EK with
its S.Part of a Joint’s Tail
and eye legs the Joint’s S.Parts?!

–dl*

77

per Dan Lehman:

No, you confuse my points in steadfastly refusing to see YOUR system's problem.
Actually, NO - there is no refusal - I don't believe there is a problem.

Your issue is how the initial 4 ‘eye knots’ are chosen.
See, I’ve just re-iterated your issue.

I had given you my answer. Here it is again:

per Mark Gommers:

One obvious answer to your paradox is that it actually doesn't matter! You can think of this in terms of 'quantum entanglement'. Imagine 2 entangled photons in a state of superposition. One photon has 'up' polarisation and the other has 'down' polarisation. If we measure one photons polarisation, we immediately know what the other photon will be.

And so the choice of 4 initial ‘eye knots’ will have a certain polarisation (polarity).
Each of these initial ‘eye knots’ will have an opposite polarisation, where the
S.Parts and Tail ends undergo a transposition and change identity.

So thats one answer to your question (ie it doesn’t matter).

Another way to answer your question (which I more strongly lean toward):

The initial 4 ‘eye knots’ will be the most logical choices.
That is, the particular choices of orientation will be guided by how closely
they align with the parent bend in terms of loading profile.
This can be viewed as homogeneity relative to the parent bend.
And so this guides the choices made.

Some of the derived ‘eye knots’ will be homogenous to the parent bend.
Some wont.
Selecting on the basis of achieving homogeneity is logical.

Please examine the attached photo below.
I have chosen 2 well known ‘bends’ as examples to illustrate my position.

For the Zeppelin bend:
I have derived Z1 and Z2 ‘eye knots’.

For the Butterfly bend:
I have derived B1 and B2 ‘eye knots’.

In my view, ‘Z1’ and ‘B1’ are the logical choices.
Furthermore, they are homogenous to their respective parent bends.
I would go as far as to suggest that you would also logically choose ‘Z1’
and ‘B1’ as your initial selection of the 4 eye knots derived from the 4 available linkages.

NOTE:
I am no longer using the terms ‘principal’ and ‘primary’.
Instead, I have advanced ‘homogenous’ to describe the derived
eye knots which more closely align to the parent bend.

Bends_Transpositions_WEB.jpg

78

Why did you stop with just two, and not the Fab Four
you keep asserting?

And AGAIN --answer this, please-- ::
Now, about the other Two of
the Fab Four.

Which is more “logical” : an EK with
its S.Part one of the Joint’s,
and eye legs the Joint’s Tails;
or an EK with
its S.Part of a Joint’s Tail
and eye legs the Joint’s S.Parts?!

[u]NOTE:[/u] I am no longer using the terms 'principal' and 'primary'. Instead, I have advanced 'homogenous' to describe the derived eye knots which more closely align to the parent bend.

Noted. BUT what are you using? “Homogeneity” has so far meant
a specific case of EK having e2e S.Part with REL = other_e2e S.Part;
other linkages have no specified standing, and you are just saying
“Choose them as you feel fit” or such.

–dl*

79

Please reference the attached image below.
Butterfly ‘bend’ and 8 corresponding ‘eye knots’.

My current best theoretical model: (this overrides all previous models)

  1. For any given end-to-end join (‘bend’), there are 4 available linkages between the S.Parts and Tail ends.
  2. A total of 8 corresponding eye knots can be derived from these 4 linkages.
  3. Some of the derived eye knots may be homogenous to the parent bend.
    Note: Not all derived ‘eye knots’ will be stable (ie unviable) - this being related to choice of S.Part
  4. For each available linkage, 2 corresponding ‘eye knots’ are possible (a geometric pairing).
    In each of these geometric pairings, one will be a transposition of the other - where the polarity has been reversed to change the identity of the S.Part and Tail end.
    In many instances, only one of these geometric pairings will be stable (viable).
  5. The corresponding ‘eye knots’ that are homogenous relative to the parent bend will meet the following criteria:
    5.1) The S.Part is congruent with an S.Part from the parent bend.
    5.2) One leg of the ‘eye’ is congruent with an S.Part from the parent bend.
    If both of these conditions are met, the derived ‘eye knot’ is homogenous.

With respect to the attached image (Butterfly bend):
a) A total of two derived ‘eye knots’ are homogenous relative to the parent bend (‘A1’ and ‘B1’ are homogenous).
b) ‘A1’ and ‘A2’ are a geometric pair.
c) ‘B1’ and ‘B2’ are a geometric pair.
d) ‘C1’ and ‘C2’ are geometric identical twins - when tied mid-line
e) ‘D1’ and ‘D2’ are geometric identical twins - when tied mid-line.

Note: C1 + C2, and D1 + D2, are ‘TWATE’ (Tiable Without Access To an End).
This property gives rise to their identical twin status.
However, they can be tied end of line (so there is the presence of a distinct tail end).
When tied end of line, there will be a distinct S.Part and Tail end (which can be transposed to reverse polarity).

Each end-to-end join (‘bend’) will have 4 available linkages (as above).
The characteristics of the derived ‘eye knots’ will be different for each ‘bend’.
‘Bends’ will be:
asymmetric
symmetric
offset
A lot of work needs to be done to explore the characteristics of the derived ‘eye knots’ from
each type of bend.
For example, some ‘bends’ produce a set of identical twin ‘eye knots’, while others do not.
The must be some underlying basis for this - which currently eludes me.

Butterfly_8 Transpositions_WEB.jpg

80

Ah, good to have a clean break & noted basis!

1. For any given end-to-end join ('bend'), there are 4 available [b]linkages [/b]between the S.Parts and Tail ends. 2. A total of 8 corresponding eye knots can be derived from these 4 linkages. 3. Some of the derived eye knots may be [i]homogenous [/i]to the parent bend. [u]Note[/u]: Not all derived 'eye knots' will be stable (ie unviable) - this being related to choice of S.Part
I think you want to say "two ... will be homogenous" --how otherwise? And also "SOME derived ... might not be stable" --but sometimes all ARE. (And "unviable" => "viable"; or "(some might be unviable)" ?! )
4. For each available [b]linkage[/b], 2 corresponding 'eye knots' are possible (a geometric pairing). In each of these geometric pairings, one will be a [i]transposition [/i]of the other - where the polarity has been reversed to change the identity of the S.Part and Tail end.
And these will of course also be what you're calling "identical twins" --that is the tangle instantiated with a connection of eye legs but otherwise awaiting the completion of the loading profile.
5. The corresponding 'eye knots' that are [b]homogenous [/b]relative to the parent bend will meet the following criteria: 5.1) The S.Part is congruent with an S.Part from the parent bend. 5.2) One leg of the 'eye' is congruent with an S.Part from the parent bend. If [i]both [/i]of these conditions are met, the derived 'eye knot' is [b]homogenous[/b].
Speaking this way makes it all sound too much like a tangle-by-tangle investigation, rather than --what it IS-- stating the logically obvious. The h. EKs are those with an Joint S.Part and the other Joint S.Part as its Ret.Eye Leg.
[u]With respect to the attached image (Butterfly bend):[/u] ... b) 'A1' and 'A2' are a geometric pair. c) 'B1' and 'B2' are a geometric pair.
And are geometric identical twins --or why not? (You've cut their tails short which affects a look, but they are the tangle with same linkage & just differing Loading Profiles. --as for C & D)
A lot of work needs to be done to explore the characteristics of the derived 'eye knots' from each type of bend.
I still see no reason to work from a Joint to other knots (currently just EKs), rather than exploring the Tangle of some knot via-a-vis a full range of Loading Profiles. Which doesn't to my thinking so far save us from much of what we struggle with !! (... such as "stability" which I think will differ from knotted material to different knotted material and also loading force).

AND to what purpose do we seek to put some formal
system as these? I’m thinking that it will help A BIT
in cataloguing knots, but believe that it is not an
assured determination of that, alas.

I’m willing to accept (as though I’ve a choice! :slight_smile:
that the system will be incomplete/imperfect,
if it can nevertheless do some helpful work.
(tho’ in producing heretofore unknown, “new” knots
–thus adding to our huge heap of knots–,
I don’t find THAT “helpful”! :slight_smile:

–dl*