The relationship between 'bends' and eye knots

Knotting Concepts & Explorations
81

To Dan Lehman:

There are aspects to this theoretical model which I need to clarify with you:

I think you want to say "two ... will be homogenous" --how otherwise?
In a general sense, I cant say with certainty that there will always be 2 homogenous derived 'eye knots'. It is not always the case, that 2 'eye knots' will be homogenous.
And also "SOME derived ... might not be stable" --but sometimes all ARE. (And "unviable" => "viable"; or "(some might be unviable)" ?! )
And here we are examining English grammar. It is true and factual to state that some derived 'eye knots' may be unstable. In other words, there is no guarantee that all derived 'eye knots' will be stable. Indeed, some may be unstable.
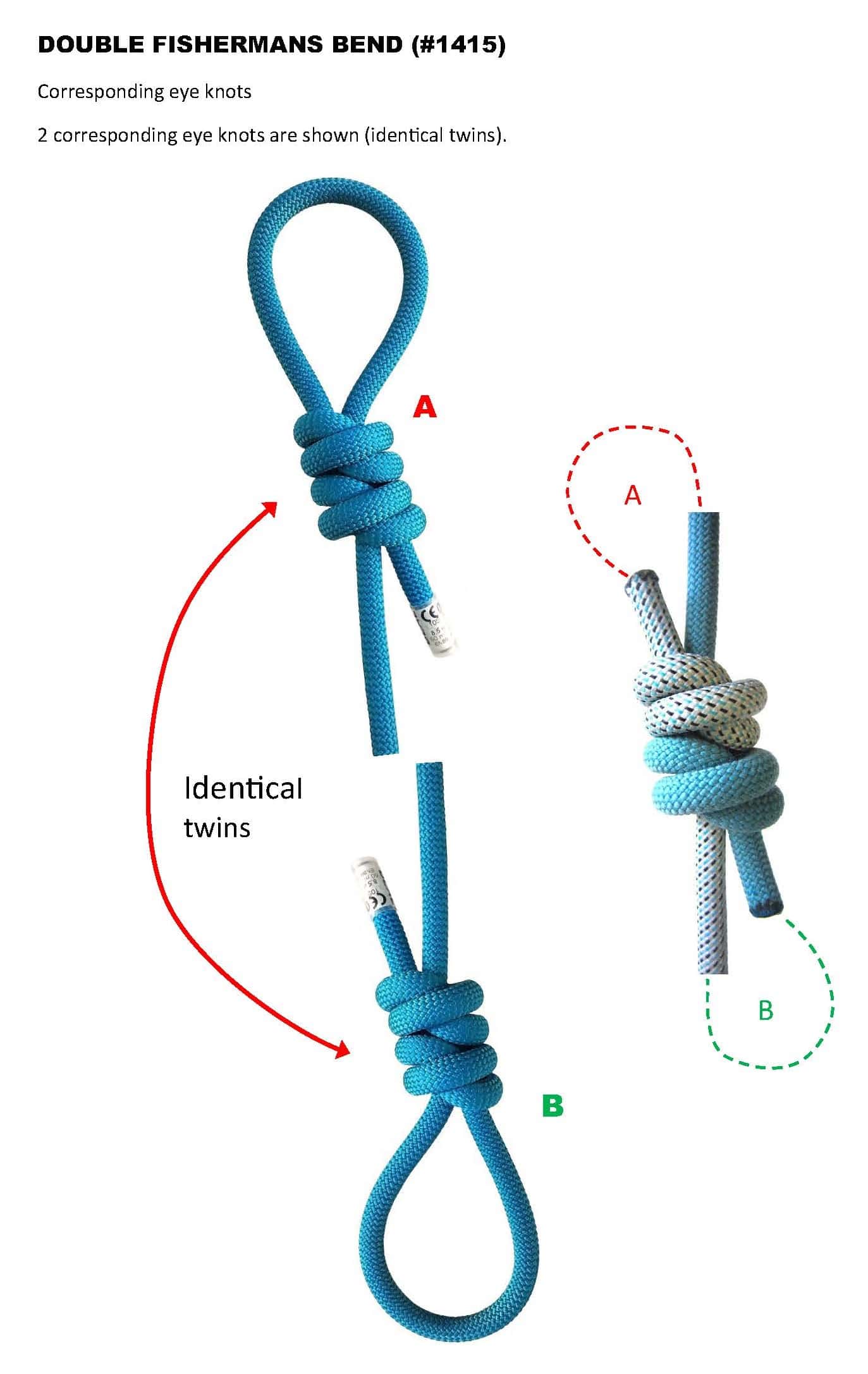
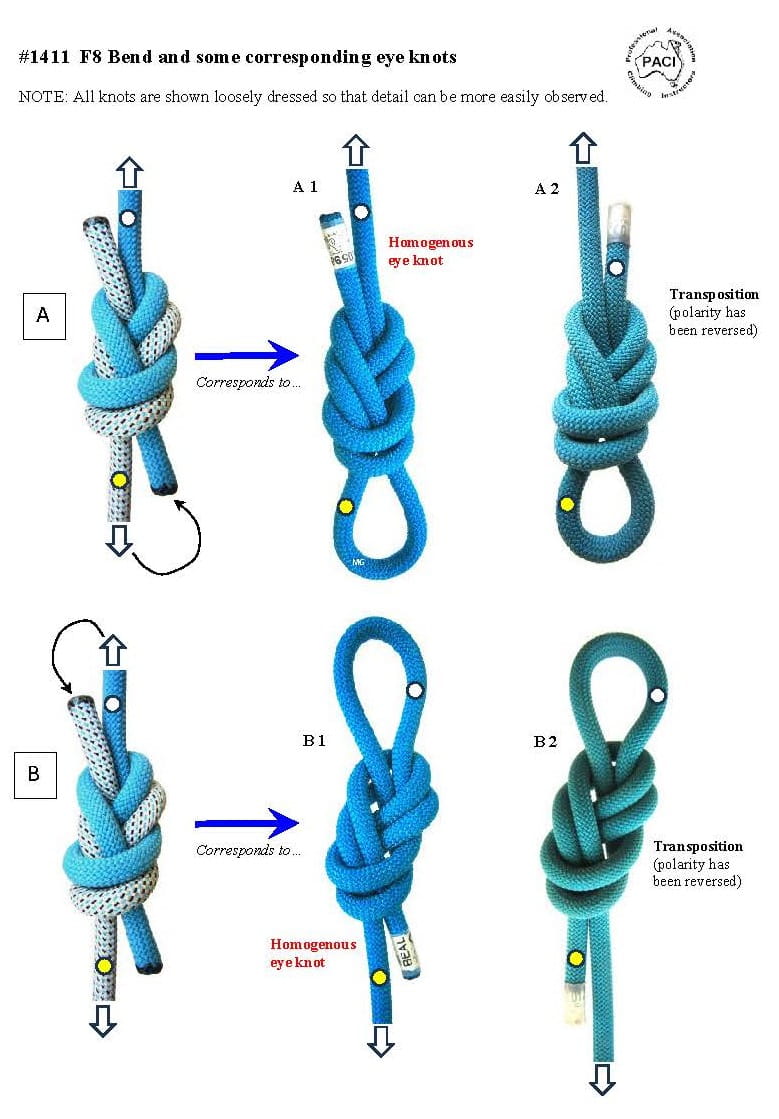
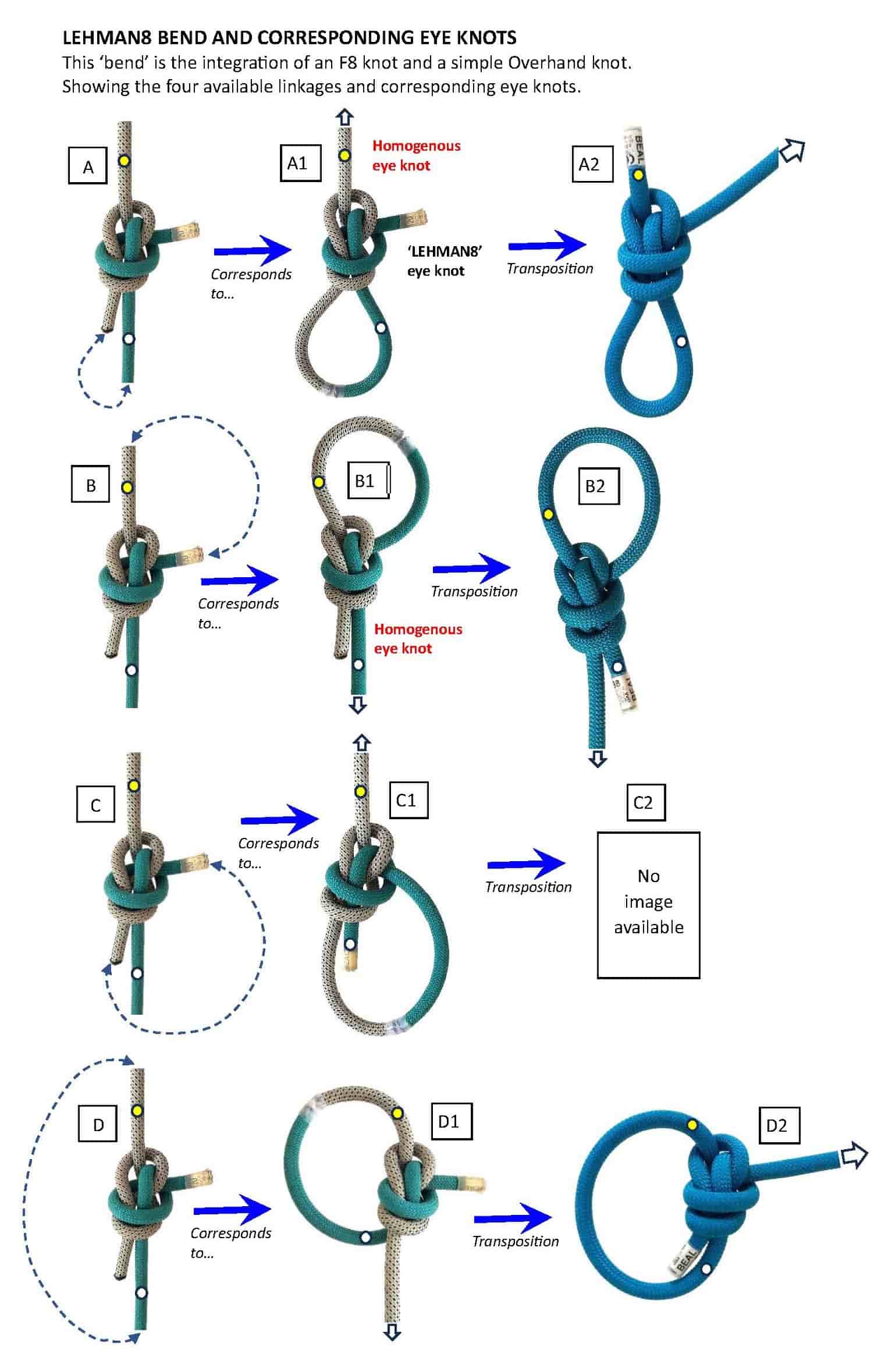
And these will of course also be what you're calling "identical twins" --that is the tangle instantiated with a connection of eye legs but otherwise awaiting the completion of the loading profile.
NO. The 'geometric pairings' are not necessarily identical twins. Please refer to the attached images for my position on this. Note that the [i]identical twins[/i] 'eye knots' occur with #1415 Double Fishermans bend. With #1411 F8 bend, there are no identical twins.

The ‘geometric pairings’ is simply my placeholder description for the 2 ‘eye knots’ that are derived from a linkage.
For each geometric pair, one is the transposition of the other.

I reserve the term ‘identical twins’ for ‘eye knots’ that are 100% identical in every aspect.
This includes S.Parts and Tail ends being congruent with each other.

Speaking this way makes it all sound too much like a tangle-by-tangle investigation, rather than --what it IS-- stating the logically obvious.
Hmmm, given the back and forth arguments with me largely repeating the same things but in different words, having clear and unambiguous definitions seem to be what you prefer. You engage in debate based on construction of the the English language (language is important). I prefer tight definitions (eg defining what a 'Bowline' is).

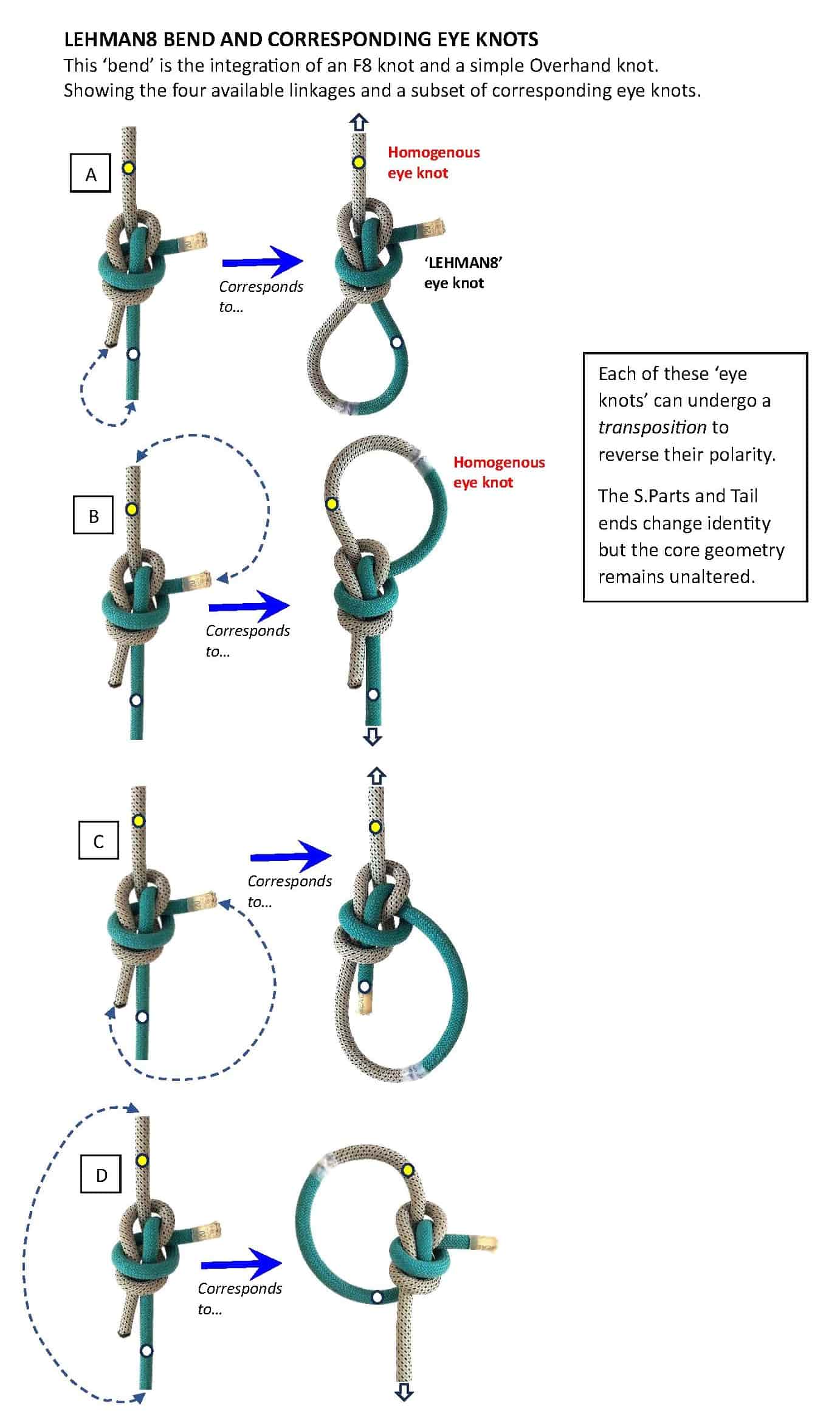
I advanced the term ‘homogenous’ to identify those derived ‘eye knots’ that align closely with the parent bend.

And are geometric identical twins --or why not?
I distinguish between a [i]geometric pair[/i] and [i]identical twins[/i]. There is a difference. Identical twins 'Eye knots' must be identical in every aspect (including S.Part and Tail end). Refer to the attached images: Note that #1415 Double Fishermans produces a set of identical twins 'eye knots'. And yet, #1411 F8 Bend does not (no identical twins). Both 'bends' are symmetric (they are not asymmetric). Why is this so? I'm going back and examining other symmetric bends - to see where and why identical twins occur... [u]Hypothesis:[/u] I posit that [i]identical twins[/i] 'eye knots' can only occur from parent bends that are [u]symmetric[/u]. I don't think it can occur with [i]asymmetric [/i]bends. What are your thoughts?

…

I still see no reason to work from a Joint to other knots (currently just EKs),
Well this is the basis of my theoretical analysis - and the title of my work. I am exploring the relationship between 'Bends' and corresponding 'eye knots'. For me, it is a logical way of exploring relationships between certain classes of knots.

We’ve been down this path several time before - and I pointed out that there is nothing
to stop you from exploring other relationships (eg start with an ‘Eye knot’ instead of a ‘Bend’).

AND to what purpose do we seek to put some formal system as these? I'm thinking that it will help A BIT in cataloguing knots, but believe that it is not an assured determination of that, alas.
The [i]purpose [/i]is the seeking of knowledge and understanding. I have never claimed that my theoretical work will solve all knot riddles and mysteries. Harry Asher made a start a long time ago - but stopped short of diving deep into the underlying theory.

I noticed that no one had really made a substantial effort to explore this subject area.
Not even the great Xarax went into any great technical detail.
(He knew about it and had made several comments in various posts, but he never fully
evolved a theoretical model).

EDIT NOTE:
You will note that I had abandoned the notional concept of 4 corresponding ‘eye knots’,
instead - stating that for each available linkage, there is a geometric pair.
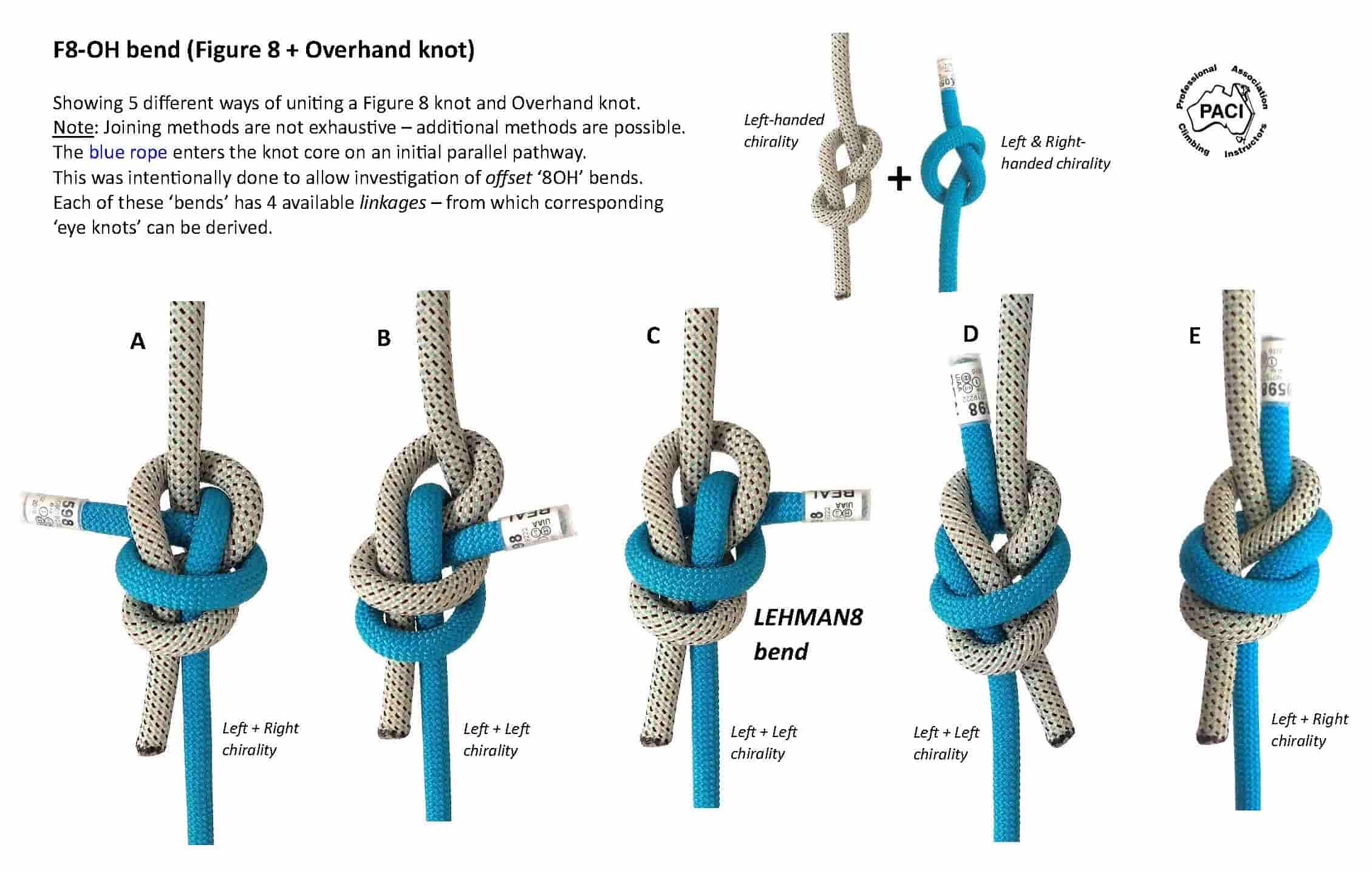
This gives rise to a total of 8 possible derived ‘eye knots’ from a given parent bend.
Your arguments made me realise that it was hard to write down a theory to support
my preference for 4 ‘eye knots’ in relation to 4 linkages.
To be perfectly honest, it is hard for the lay person to grasp that there are 8 possible combinations
of ‘eye knots’. It is easier to simply say “there are 4 derived ‘eye knots’ corresponding to the 4
available linkages”.
It gets complicated to talk about all of the possible combinations.
Furthermore, some of these derived ‘eye knots’ are illogical - from the point of view
of loading profile and stability.
I evolved the theory of the transposition to help explain how there are 8 possible combinations
of corresponding ‘eye knots’.

Dan - I note that you like to sit back and let me do all the ‘hard yards’ of developing the theory,
by barking at appropriate moments. You don’t seem to offer up your own theory or help to improve my theory?
I do all the hard work producing high quality photo images - you provide exactly zero images.
And yet, I plod onwards like a good soldier putting up the good fight.

It would be nice to see you advance some theories!

DOUBLE FISHERMANS BEND_Corresponding eye knots_identical twins_WEB.jpg

F8-Bend_2 corresponding_eye-knots_WEB.jpg

82

I repeat :: How can it possibly be otherwise?!

And also "SOME derived ... might not be stable" --but sometimes all ARE.
(And "unviable" => "viable"; or "(some might be unviable)" ?! )
And here we are examining English grammar. It is true and factual to state that some derived 'eye knots' may be unstable. In other words, there is no guarantee that all derived 'eye knots' will be stable. Indeed, some may be unstable.
Not grammar, but diction :: your parenthesis attaches to "stable" and thus it is "viable" that matches that; you must be thinking the entire phrase "might not be s." = "([and so be] UNviable)"
And these will of course also be what you're calling "identical twins" --that is the tangle instantiated with a connection of eye legs but otherwise awaiting the completion of the loading profile.
NO. The 'geometric pairings' are not necessarily identical twins. Please refer to the attached images for my position on this. Note that the [i]identical twins[/i] 'eye knots' occur with #1415 Double Fishermans bend. With #1411 F8 bend, there are no identical twins.
???! We've been down this path previously, with you ultimately abandoning this now repeated assertion. The knots ARE the same, coming from the symmetric tangle of the parent. I can't understand how you aren't seeing this --you who are making (the quite good!) images!??
I reserve the term 'identical twins' for 'eye knots' that are 100% identical in every aspect. This includes S.Parts and Tail ends being [i]congruent [/i]with each other.
And this isN'T the case with the Butterfly, which is asymmetric, but which you claim twinness for case C2.
I advanced the term 'homogenous' to identify those derived 'eye knots' that align closely with the parent bend.
But you need only take a Tangle PoV and state the Loading Profile --for which there is no mystery or seek-&-find but obvious Loading positions.
And are geometric identical twins --or why not?
I distinguish between a [i]geometric pair[/i] and [i]identical twins[/i]. There is a difference. Identical twins 'Eye knots' must be identical in every aspect (including S.Part and Tail end). Refer to the attached images: Note that #1415 Double Fishermans produces a set of identical twins 'eye knots'. And yet, #1411 F8 Bend does not (no identical twins). Both 'bends' are symmetric (they are not asymmetric). Why is this so?
Again, the knots ARE the same --they have to be (so, too, the single & other multiple Fisherman's, & on & on.).

…

I still see no reason to work from a Joint to other knots (currently just EKs),
Well this is the basis of my theoretical analysis - and the title of my work. I am exploring the relationship between 'Bends' and corresponding 'eye knots'. For me, it is a logical way of exploring relationships between certain classes of knots.

The Tangle gives you the entire intertwined entity,
and you can seek however you want from that.

short of time ::: YES, I’m lame in advancing …,
because I am hard ON MYSELF TOO, and just have
trouble getting anywhere!!

–dl*

83

To Dan Lehman:

Quote
I think you want to say "two ... will be homogenous" --how otherwise?
In a general sense, I cant say with certainty that there will always be 2 homogenous derived 'eye knots'. It is not always the case, that 2 'eye knots' will be homogenous.
I repeat :: How can it possibly be otherwise?!
Answer: Its because we are using different definitions and interpretations of language. This is always the case when debating these types of matters... it comes down to how we define things. ... OK: When I use the term 'identical twins' - I mean identical in all aspects, including position of S.Part and Tail end.

Note:
I also advanced the term ‘Geometric pair’ (and geometric pairing).
A geometric pair is/are not identical twins.
Only ‘identical twins’ are identical in every way.
Definition:
A geometric pair is where 2 knots share the same common core geometry.
However, the S.Parts and Tail ends are not in the same positions (they are transposed).

I’m going to assume that this definition is the root cause of any misunderstanding.

More notes for you:
Thus far, I have only found three (3) different ‘bends’ that produce
‘identical twins’ ‘eye knots’. They are:

  1. Double Fishermans bend (Ashley #1415)
  2. Ring/Water bend (Ashley #1412)
  3. Riggers bend (Ashley #1425A).
    I believe the reason is because both ends of the joint are in fact identical.
    Perhaps these ‘bends’ are the true symmetric bends?

The Zeppelin bend does not produce identical twins ‘eye knots’.
Although most declare the Zeppelin bend to be ‘symmetric’ - however,
it has point inversion symmetry.

…

Again, the knots ARE the same --they have to be (so, too, the single & other multiple Fisherman's, & on & on.).
Again - we are applying different definitions of what constitutes 'identical'. Yes - the Double Fishermans bend (Ashley #1415) does produce a set of identical twins eye knots. Note that the Zeppelin bend does [u]not[/u]. I distinguish between the term 'geometric pair' and identical twin'. I have a strong feeling that you are applying a different definition.
84

And I’m not here talking about “identical twins”,
but on the logical situation of how many “homogenous”
EKs are derivable. There MUST BE two & only two.
What case do you think shows otherwise?!

[u][b]Note:[/b][/u] [u]Definition:[/u] A [i]geometric pair[/i] is where 2 knots share the same common [i]core [/i]geometry. However, the S.Parts and Tail ends are not in the same positions (they are transposed).

I’m going to assume that this definition is the root cause of any misunderstanding.

More notes for you:
Thus far, I have only found three (3) different ‘bends’ that produce
‘identical twins’ ‘eye knots’. They are:

  1. Double Fishermans bend (Ashley #1415)
  2. Ring/Water bend (Ashley #1412)
  3. Riggers bend (Ashley #1425A).
    I believe the reason is because both ends of the joint are in fact identical.
    Perhaps these ‘bends’ are the true symmetric bends?

As I said above, so too are ALL of the single/double/triple… Fisherman’s
series. And the Fig.8 joint, and so on & on.
The Zeppelin bend [i]does not[/i] produce identical twins 'eye knots'. Although most declare the Zeppelin bend to be 'symmetric' - however, it has [i][b]point inversion symmetry[/b][/i].
By virtue of opposite handedness of S.Parts.

…

Again, the knots ARE the same --they have to be (so, too, the single & other multiple Fisherman's, & on & on.).
Again - we are applying different definitions of what constitutes 'identical'. Yes - the Double Fishermans bend (Ashley #1415) does produce a set of identical twins eye knots. Note that the Zeppelin bend does [u]not[/u].
Note that I pointed to THEntire Fisherman's SERIES! Don't bring Thrun's Joint, but address the stated case, the series.

–dl*

85

per Dan Lehman:

And I'm not here talking about "identical twins", but on the logical situation of how many "homogenous" EKs are derivable. There MUST BE two & only two. What case do you think shows otherwise?!
One thing I have learned is not to jump to conclusions without solid evidence. There are indeed cases where there is only one [i]homogenous [/i]derived 'eye knot'. Example: Sheet Bend (Ashley #1431). The Sheet Bend does [u]not [/u]produce 2 [i]homogenous [/i]'eye knots'
As I said above, so too are ALL of the single/double/triple... Fisherman's series. And the Fig.8 joint, and so on & on.
Dan - I stated "thus far"... meaning that I haven't checked and confirmed beyond what I indicated. Yes - I am fairly sure that more end-to-end joins ('bends') will produce sets of identical twins 'eye knots'.

With specific regard to the Double Fishermans and the other same genus variations:
Yes, we can posit that a Single Fishermans, Double Fishermans, Triple Fishermans (etc) will all produce
sets of identical twins corresponding ‘eye knots’.
You’re not declaring anything revolutionary or ground-breaking here!
That’s because these joints are all of the same genus.

And the Fig.8 joint,
No - not the F8 bend (Ashley #1411). It does [u]not [/u]produce sets of identical twins 'eye knots'. However, it does produce two (2) homogenous corresponding 'eye knots'.

This is where I am trying to be careful with definitions and language.

Again:
Double Fishermans bend (Ashley #1415) produces a set of identical twins ‘eye knots’.
Figure 8 bend (Ashley #1411) does not produce a set of identical twins ‘eye knots’.
However, both of these ‘bends’ do produce 2 homogenous corresponding ‘eye knots’.

I would posit that all interpenetrating symmetric joints (‘bends’) will produce sets
of identical twins corresponding ‘eye knots’.
The Double Fishermans bend (Ashley #1415) is an example of an interpenetrating
symmetric joint.

It is of interest to me why the F8 bend (Ashley #1411) does not produce sets of identical twins
‘eye knots’ (in comparison to Double Fishermans bend (Ashley #1415 which does).
Roger Miles would have claimed that both joints (‘bends’) are symmetric.
But, there is a unique property to the Double Fishermans bend that sets it apart.

Roger Miles did not investigate this.
Neither did Harry Asher.
I dont think anyone has written down a theory to demonstrate and explain this aspect of ‘bends’.
And neither has Dan Lehman…

86

THIS is a logical matter occurring [i]'a priori[i]
–not some empirical study!

There are indeed cases where there is only one [i]homogenous [/i]derived 'eye knot'. Example: Sheet Bend (Ashley #1431). The Sheet Bend does [u]not [/u]produce 2 [i]homogenous [/i]'eye knots'
??! Of course it DOES --the parent Joint' U-fold S.Part is that of the h. EK, and the parent's other S.Part is the RELeg of this 2nd h. EK. QED. (No empirical search for "evidence" involved.)
As I said above, so too are ALL of the single/double/triple... Fisherman's series. And the Fig.8 joint, and so on & on.
Dan - I stated "thus far"... meaning that I haven't checked and confirmed beyond what I indicated.
You cannot be this daft :: it is readily perspicuous that any change in this OH series of pull-together knots will see the same relation in EK formation --one simply alters the particular tangle OH components, which changes nothing re homogeneity.

With specific regard to the Double Fishermans and the other same genus variations:

Yes, we can posit [KNOW!] that a Single Fishermans, Double Fishermans, Triple Fishermans (etc) will all produce sets of identical twins corresponding 'eye knots'. You're not declaring anything revolutionary or ground-breaking here!
Then PLEASE stop all this ranting about the [i]Grapevine bend[/i] being a special case and all so puzzling --it's NEITHER.
I would posit that all interpenetrating symmetric joints ('bends') will produce sets of identical twins corresponding 'eye knots'. The Double Fishermans bend (Ashley #1415) is an example of an [i]interpenetrating symmetric joint[/i].
And similarly you should be able to know that this assertion if false --the pull-together knots might use opposite-handed like structures (as we see likely in mistaken imagery from time to time for the [i]Grapevine[/i]).

–dl*

PS : “And neither had Dan Lehman”
who remembers discussing the supposed amazing & so-far
unique twinning of the Grapevine from a slightly older (October)
thread, quoting … ::

87

Dan,
It would be easier to debate the intricacies of this theoretical exposition
if you refrained from ad hominem verbiage.

With regard to the Sheet bend (Ashley #1431):
Please refer to the attached image (below).
There are 4 available linkages, and I have derived 4
logical corresponding ‘eye knots’.
And here I use the term ‘logical’ - because they are indeed
the obvious and logical choices to be made.
You may wish to make an argument that they are not the logical choices.
I would challenge you to advance a convincing argument that points to
my 4 choices being illogical.

Now - we know that each of these 4 derived ‘eye knots’ can undergo
a transposition to reverse their polarity.
However, instability occurs.
In fact most transform into gnat hitches - ie, they are no longer ‘eye knots’.
I do not regard a gnat hitch or a variant gnat hitch to be an ‘eye knot’.
A gnat hitch is a type of noose.
This topic thread is about corresponding ‘eye knots’ - not noose hitches.
Reversing the polarity in a transposition places the derived structures
into a different realm - something other than ‘eye knots’.
Although I would concede that the noose hitches are nevertheless
derived from the parent bend, and this pushes the theory into new unexplored areas.

In my view, the Sheet Bend only produces 1 homogenous ‘eye knot’ (#1010 Simple Bowline).
This corresponds to image “A” in my photo below.

…

You cannot be this daft
Your ad hominem reference to daftness and being "daft" is misplaced. I was simply stating my position - and that is I prefer to look at the evidence. There are too many nuances and variables with 'bends' and 'eye knots' - and its risky to jump to conclusions.
Then PLEASE stop all this ranting about the Grapevine bend being a special case and all so puzzling --it's NEITHER.
Another ad hominem remark. Look, the Double Fishermans bend (Ashley #1415) does produce a set of identical twins 'eye knots' - that's a factual statement. Your reference to a discordant Double Fishermans (where the chirality of one 'strangled' double overhand knot has been reversed) is an entirely different matter - why raise it? Note: The 'discordant' variant doesn't produce a set of identical twins 'eye knots'.

This comes down to how we each understand what a ‘knot’ is.
In my personal view, a hand tied knot will have a very specific geometry,
and that gives it distinctiveness (its uniqueness).
If you change something - then you change the identify of the knot into something else.

If I held up Ashley #1053 and asked you to identify it - you would (more likely than not)
claim that it is a “Butterfly” eye knot.
If I held up Ashley #1010, you would likely identify it as a simple “Bowline”.
This is the dilemma of a knot assessor when assessing a student knot tyer.
If the assessor asks a student to tie and present a Double Fishermans bend (Ashley #1415),
and the student presents a discordant Double Fishermans, is that a pass or fail?
Technically, it must be a ‘fail’ - because it isn’t #1415.

The discordant Double Fishermans is not Ashley #1415.
We can say that it is related - but we cant say that it is identical to #1415.
per Dan Lehman:

And similarly you should be able to know that this assertion if false --the pull-together knots might use opposite-handed like structures (as we see likely in mistaken imagery from time to time for the Grapevine).
Again, a discordant Double Fishermans is not #1415. It is something else - it is related (same genus/family) but not same species. I was originally focussed only on #1415 - [i]not [/i]its discordant relative. And the 'discordant' variant doesn't produce a set of identical twins 'eye knots'. I did posit that interpenetrating symmetric 'bends' might be likely to produce identical twins 'eye knots'. In my view, a discordant Double Fishermans is not 'symmetric' - and so this might explain why it doesn't produce a set of identical twins 'eye knots'.

…

PS : "And neither had Dan Lehman" who remembers discussing the supposed amazing & so-far unique twinning of the Grapevine from a slightly older (October) thread, quoting ... ::
I was commenting in relation to the broader underlying theory of 'bends' and corresponding eye knots. Harry Asher made a very basic intro in his book (The Alternative Knot Book). Ashley himself was largely silent on the matter - only a few references appear in his book - but nothing substantial. I think there is a lot more to know and understand. Eg Some end-to-end joins (bends) produce identical twins 'eye knots' while others don't. Note that #1425A Riggers bend does produce as set of identical twins 'eye knots' (but Zeppelin bend does not). And yes, I already corrected my initial claim that #1415 produces 2 sets of identical twins 'eye knots'. We know that it does not - instead - only 1 pair of identical twins. I find the whole subject area very interesting - and I think further discoveries await...

Sheetbend_Corresponding-eyeknots_WEB.jpg

F8-OH bends_WEB.jpg

88

Showcasing the ‘Lehman8’ bend and corresponding eye knots.
There are 4 available linkages, and 4 corresponding eye knots are shown.

The ‘Lehman8’ is derived from image ‘A’ at top.
This ‘eye knot’ is homogenous with respect to the parent bend.
Unfortunately, none of these structures are ‘TWATE’ (Tiable Without Access To an End).

Note that the ‘eye’ in image “D” can be oriented to the right. The shown orientation
is simply how I chose to set it for the photograph.

Obviously, all knots are shown loosely dressed for ease of examination.

“C” is interesting: It is stable and secure and might be jam resistant.
Testing is required to confirm this hypothesis.
I prefer “C” in comparison to “A” (the Lehman8).

“D” can also be transposed - reversing its polarity - to produce an interesting eye knot.

LEHMAN8 BEND AND CORRESPONDING EYE KNOTS_WEB.jpg

89

I have one minor question concerning how you selected the “4 principal eye knots” in your diagram in Reply 87 of the Lehman8 Bend. When I have done this in the past, I have picked one “color” and made it the standing part in all of the first set (or principal) eye knots. For example, you chose the white rope for the standing part in A, C, and D, but not in B. Of course, when you take transpositions, you will get all of the rest. I just wondered how you had selected the knots in you “principal” list.

90

But this begs the question of Why are THESE knots “principal”?!
–and others come by some “transposition” process!?
As opposed to just generating the entire 8 (of a 2-tangle)
and calling them on their interelations as desired.

Mark of course finds stronger matching in the EKs that
take one of the Joint’s S.Parts AND use the other S.Part
as the RELeg --so, both parent S.Parts & one as EK S.Part
–which puts each S.Part of the Joint into that position in the EK.

–dl*

91

per Dennis Pence:

I have one minor question concerning how you selected the ?4 principal eye knots? in your diagram in Reply 87 of the Lehman8 Bend.
Dennis, I didn't declare any of the derived 'eye knots' to be [i]principal[/i]! I ceased using the terms 'principal' and 'primary' some time ago - finding a better way to conceptualise relationships to the [u]parent bend[/u] via [i][b]homogeneity[/b][/i]. [u]Key concept here:[/u] 1. There is a parent 'bend' 2. The derived 'eye knots' are geometrically related to their parent bend. 3. There are four available [i]linkages [/i]between the S.Parts and Tail ends. 4. How these 'linkages' are exploited can be contentious, when only 4 choices are initially made (as I had done). I had argued this salient point with Dan - stating that some choices are more logical than others. Indeed, some [i]transpositions [/i]result in instability - where the derived 'eye knot' is not viable.

The ordinary dictionary meaning of homogenous more closely aligns with my intent.
And so with respect to the Lehman8 bend:

  1. There are two homogenous corresponding ‘eye knots’
  2. The original ‘Lehman8’ ‘eye knot’ was discovered by Dan Lehman many years ago - but his discovery was not via the systematic method I am employing here. His principal design goals were; jam resistance, and security. The Lehman8 is not ‘TWATE’ (Tiable Without Access To an End) - so Dan started with a simple F8 knot and then figured out a way of integrating a simple Overhand knot with the F8 - in order to achieve his design goals.
  3. The derived ‘eye knots’ (A, B, and C from the Lehman8 bend) are logical choices - and “D” being merely one choice out of 2 possibilities.

I had defined the concept of homogenous (and homogeneity) in a previous post.
Suffice to quickly summarise: A homogenous derived ‘eye knot’ more closely aligns to its parent bend in terms of load segments.
The S.Part is congruent to an S.Part of the parent bend.
And one leg of the ‘eye’ is congruent with the opposite S.Part of the parent bend.

When I have done this in the past, I have picked one ?color? and made it the standing part in all of the first set (or [b]principal[/b]) eye knots. For example, you chose the white rope for the standing part in A, C, and D, but not in B.
Again - I never used the term [i]principal [/i]- preferring instead the term 'homogenous'. With respect to derived 'eye knot' "B" - the choice of the [b]blue [/b]rope results in a closer alignment with respect to the parent bend. The [b]blue [/b]rope corresponds to the S.Part of the parent bend - and so, this choice results in homogeneity. If you look closely at the parent bend (ie the Lehman8 bend), the lower [b]blue [/b]rope is an S.Part. And the upper [i]white [/i]rope is the other opposite S.Part. And so the 'choice' I made is logical if one is seeking [i]homogeneity [/i]with respect to the parent bend.

I included a side text box in my image - which explains that all of the derived ‘eye knots’ can undergo a transposition to reverse their polarity.
I assume that you noticed and read the content of that text box - yes?

I would also point out that preparing all of these knots for photography is a long and tedious (and thankless) exercise.
This is likely why Dan Lehman contributes exactly zero photos - because it is time consuming and fiddly, and a largely thankless exercise.
I will eventually show all of the transpositions - but it takes more of my personal time.
As my time is limited - I can only show what I believed was more ‘obvious’ and logical.
From my point of view, the derived ‘eye knot’ “D” was a toss up - I could have made the blue end the S.Part (but I chose to make the white end the S.Part).
Again - I did point out in the side text box that each of the shown derived ‘eye knots’ can undergo a transposition.

Of course, when you take transpositions, you will get all of the rest. I just wondered how you had selected the knots in you ?principal? list.
Again: I never used the term principal! I was careful in my choice of language - because Dan Lehman had already gone to great lengths to assert his opinion with respect to how 'choices' of orientation are made. Again - all derived 'eye knots' can undergo a transposition to reverse their polarity. I didn't have time to photograph all 8 derivations! So I limited myself to what I believed were the most logical choices. And here I use the term 'logical' in the sense that the choices were based on achieving [i]homogeneity [/i]with respect to the parent bend. And the [b][i]parent bend[/i][/b] is the key concept - the derived 'eye knots' relate to their [u]parent bend[/u].

When deriving corresponding ‘eye knots’ - one needs a reference frame (a source).
The source reference frame is a particular ‘parent bend’.
In this instance, the source reference frame is the Lehman8 bend.
Using the Lehman8 bend as the ‘source’ - I then worked to derive the corresponding ‘eye knots’.
The correspondence can only have meaning relative to something - in this case - the Lehman8 bend.

Does that all make sense to you Dennis?

…

Now, on to Mr Dan Lehman:

But this begs the question of Why are THESE knots "principal"?! --and others come by some "transposition" process!?
I never used the term principal - Dennis Pence used that term (not me)!! REQUEST: Can we please cease and desist in using the term principal or primary? A few months ago, I was in search of the right language to describe the unfolding theory. The term homogeneity had not yet been used. I originally used terms such as primary and principal as placeholders to explain some concepts. I have since dropped those terms in favour of [i]homogeneity[/i].
As opposed to just generating the entire 8 (of a 2-tangle) and calling them on their interelations as desired.
Firstly, for me personally, it is a huge exercise in time and effort to prepare and photograph all 8 derivations. And it is a [u]thankless [/u]exercise. Secondly, I do believe that the choices of orientation of corresponding 'eye knots' corresponding to the 4 linkages can be made on a 'logical' basis. The original 'Lehman8' eye knot is a logical choice in my view. It is homogenous with respect to the parent bend - and it is secure and stable in loading. Yes, the 'Lehman8' eye knot can undergo a [i]transposition [/i]- which reverses its polarity. I will showcase a transposed Lehman8 when I find time. But, I initially chose not to show it - because for me - it is not a logical choice. And here I am sure we will get into arguments about 'logic' and the choices to be made. One can advance an argument that the original Lehman8 is not a logical choice - and that its transposed version is preferred. When attempting to present derived 'eye knots' to the general public and world - I find it easier to just show 4 initial corresponding 'eye knots' that logically align to the parent bend, and also with respect to the available linkages. It can get confusing when you attempt to show all 8 derivations...
92

Mark, Thank You for your contributions and clear photographs !

SS

93

Thanks Scott!
Hope you have time off over Christmas and enjoy your self…

94

I’ve done more work with the ‘Lehman8 bend’ and corresponding ‘eye knots’.
In my view, “A1”, “B1”, and “C1” are all logical derivations.
‘Logical’ in the sense that they more closely align to the parent bend.

“D1” and “D2” are a toss up as to which is more stable under loading.
Likely “D2” is the more stable orientation.

I consider “A2” to be illogical.

Be that as it may, there are 4 available linkages, and a total of 8 corresponding
‘eye knots’ relative to the parent bend.

Of all the possible derivations, I am of the view that “A1” and “C1” are both
the stand-out ‘eye knots’.
I actually lean toward “C1” as being the top pick.

Note:
I believe that “C2” would not be viable.

LEHMAN8 BEND AND CORRESPONDING EYE KNOTS_WEB.jpg